Η ακουστική υπογραφή των drones: Ανίχνευση, αναγνώριση και δυνατότητες αντιμέτρων Β μέρος. Προσπάθειες εντοπισμού drones με απλά, φτηνά και φτωχά μέσα
Γράφει ο Γεώργιος Δικαίος στις 9 Οκτωβρίου 2025

https://www.gazeta.ru/tech/news/2023/08/26/21149438.shtml
Δημιουργήθηκε ένας «έξυπνος» πίνακας μικροφώνων για την αναγνώριση drones μέσω ήχου Στο Τσερεπόβτσε εφηύραν έναν πίνακα μικροφώνων με τεχνητή νοημοσύνη για την ανίχνευση drones μέσω ήχου
Αναπτύσσω εφαρμοσμένα μαθηματικά και λογισμικό για την επεξεργασία ακουστικών σημάτων σε συστήματα επικοινωνιών. Το πρώτο μου άρθρο σχετικά με την ακουστική των drones για το Military Review ήταν κάπως απλό και δεν προκάλεσε ιδιαίτερο ενδιαφέρον αρχικά, αλλά αργότερα έγινε το μόνο από τα άρθρα μου που διαβάστηκε συστηματικά. Ως εκ τούτου, θεώρησα απαραίτητο να επανεξετάσω το θέμα, λαμβάνοντας υπόψη τα σχόλια. Αυτή τη φορά κατέβασα σημαντικά υψηλότερης ποιότητας ηχογραφήσεις από ουκρανικά drones (το "Lyut" και μικρότερα), και η κριτική μπορεί να ξεκινήσει με μια εικόνα time-lapse της ηχογράφησης από το μικρόφωνο ενός από αυτά.
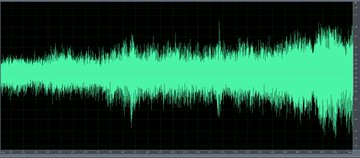
Όταν μεγεθύνουμε την εικόνα του χρόνου (παλμογράφο), μπορούμε ήδη να δούμε λεπτομέρειες που μπορούν εύκολα να ερμηνευτούν.
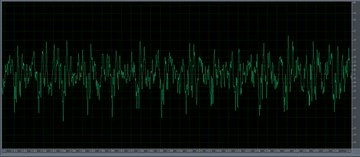
Παρά το φαινομενικό χάος, βλέπουμε ξεκάθαρα μια περίοδο κανονικών παλμών, οι οποίοι δεν είναι τίποτα περισσότερο από τους κυλίνδρους εξάτμισης των κυλίνδρων του κινητήρα. Φυσικά, για να αναλύσουμε αριθμητικά τις μετρήσεις, πρέπει ακόμα να κατανοήσουμε τον αριθμό των κυλίνδρων, τον κύκλο του κινητήρα και τον χρονισμό των βαλβίδων, αλλά αυτό το έργο είναι σαφές και αρκετά απλό.
Αυτός ο τύπος σήματος ανήκει στην αρμονική κατηγορία. Τι είναι; Κατά τη διάρκεια της εξέλιξης, η ακοή μας έχει «ακονιστεί» ώστε να αντιλαμβάνεται τρεις κατηγορίες σημάτων:
- εκρήξεις (στα αγγλικά, αυτά είναι μεταβατικά), όπως το τρίξιμο ενός κλαδιού κάτω από τα πόδια· - θόρυβοι, ένα παράδειγμα των οποίων μπορεί να είναι ορισμένα σύμφωνα· - αρμονικά σήματα, που αντιπροσωπεύονται από τα φωνήεντά μας, τους ήχους των ζώων και το κελάηδημα των πουλιών.
Ένα χαρακτηριστικό γνώρισμα των αρμονικών σημάτων είναι ότι το θεμελιώδες τμήμα τους αντιπροσωπεύει ένα περίπου περιοδικό σήμα, το οποίο είναι πολύ διαφορετικό από ένα στοιχειώδες ημιτονοειδές κύμα. Αυτό δημιουργεί μια σειρά από αρμονικές, πολλαπλάσια της θεμελιώδους συχνότητας.
Και το ίδιο σήμα στην αναπαράσταση συχνότητας θα μοιάζει με μια μάζα παράλληλων γραμμών, που ισαπέχουν από την τιμή της θεμελιώδους συχνότητας.
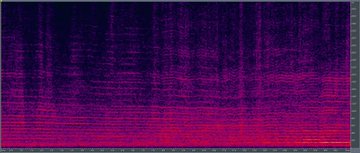
Το φάσμα του drone δεν δίνει έμφαση σε συγκεκριμένες ζώνες συχνοτήτων, όπως συμβαίνει, για παράδειγμα, με τους φωνηεντικούς ήχους της ομιλίας μας. Η κύρια ενέργεια βρίσκεται στην περιοχή κάτω από 1,5–2 kHz. Συνολικά, η ταχύτητα του κινητήρα του drone είναι αρκετά σταθερή, αν και ο ελεγκτής ταχύτητας του κινητήρα είναι αισθητός. Σε ένα drone, το φορτίο του κινητήρα είναι η έλικα, η οποία έχει ορισμένες παραμέτρους αδράνειας. Αν κοιτάξουμε τα παραδοσιακά οχήματα, ωστόσο, ο κινητήρας είναι συνδεδεμένος με τους τροχούς και το αντικείμενο αδράνειας είναι ολόκληρο το όχημα, συμπεριλαμβανομένων των επιβατών του. Τέτοιες κυματισμοί στην φασματική εικόνα προφανώς δεν παρατηρούνται εκεί. Μια πιο ακριβής εικόνα αυτού του φαινομένου απαιτεί εμβάθυνση στους μετασχηματισμούς Laplace, την κλασική θεωρία ελέγχου και σε βουνά ψηφιακών δεδομένων.

Αν πάρουμε ένα κομμάτι της φασματικής εικόνας σε οποιαδήποτε χρονική στιγμή, το φάσμα θα μοιάζει κάπως έτσι.
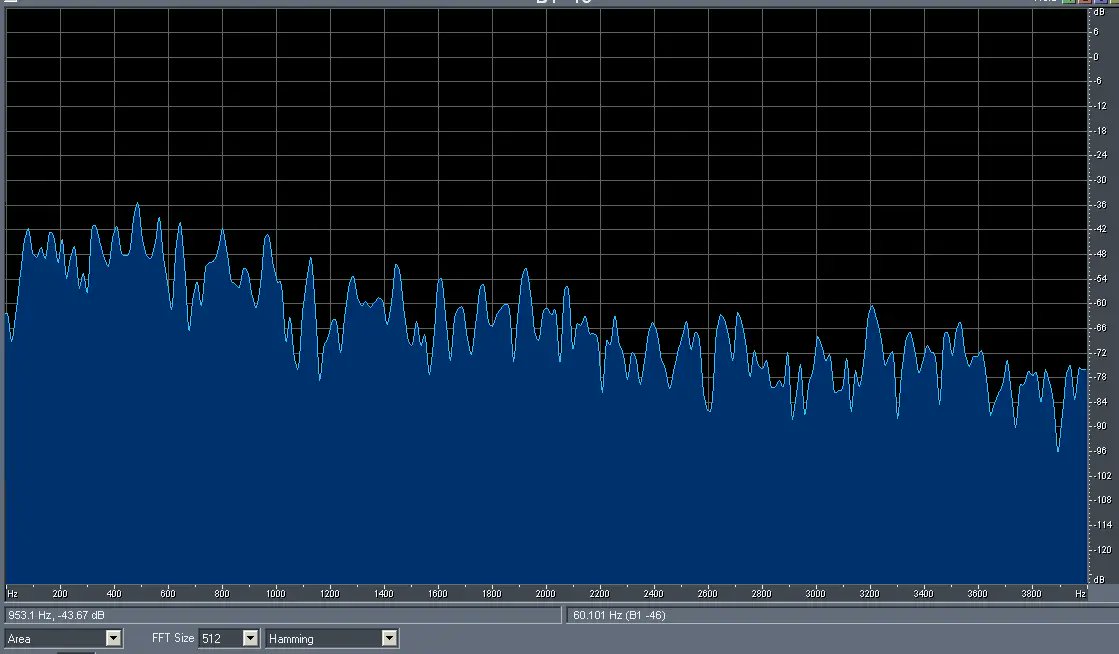
Εδώ βλέπουμε τα πλάτη των αρμονικών (σε λογαριθμική κλίμακα) σε συχνότητες που είναι πολλαπλάσια της θεμελιώδους συχνότητας. Παρεμπιπτόντως, υπάρχει ένας νόμος στη βιολογία που ορίζει ότι η αίσθησή μας είναι ανάλογη με τον λογάριθμο του μεγέθους του ερεθίσματος (για παράδειγμα, ακουστική πίεση). Η τομή που φαίνεται είναι επίσης περιοδική.
Τεχνικά, ελήφθη χρησιμοποιώντας τον μετασχηματισμό Fourier, μια εξαιρετικά χρήσιμη μαθηματική και υπολογιστική λειτουργία.
Αλλά αυτό που είναι ενδιαφέρον εδώ είναι ότι, λόγω της περιοδικότητάς της, αυτή η εικόνα μπορεί να εκτελεστεί ξανά μέσω του μετασχηματισμού Fourier. Αυτή η λειτουργία ονομάζεται κέπστρουμ και μου ζητήθηκε να τη δοκιμάσω στα σχόλια του προηγούμενου άρθρου.
Σε αυτήν την περίπτωση, ο μετασχηματισμός Fourier θα αποδώσει την περίοδο της θεμελιώδους συχνότητας των αιχμών (την απόσταση μεταξύ των αρμονικών στο φασματογράφημα, αλλά εκφρασμένη σε αντίστροφη συχνότητα - την περίοδο). Αυτό μας επιτρέπει να μηδενίσουμε αυτόματα ένα δεδομένο αρμονικό σήμα και να εξαγάγουμε συμπεράσματα σχετικά με την ταυτότητά του.
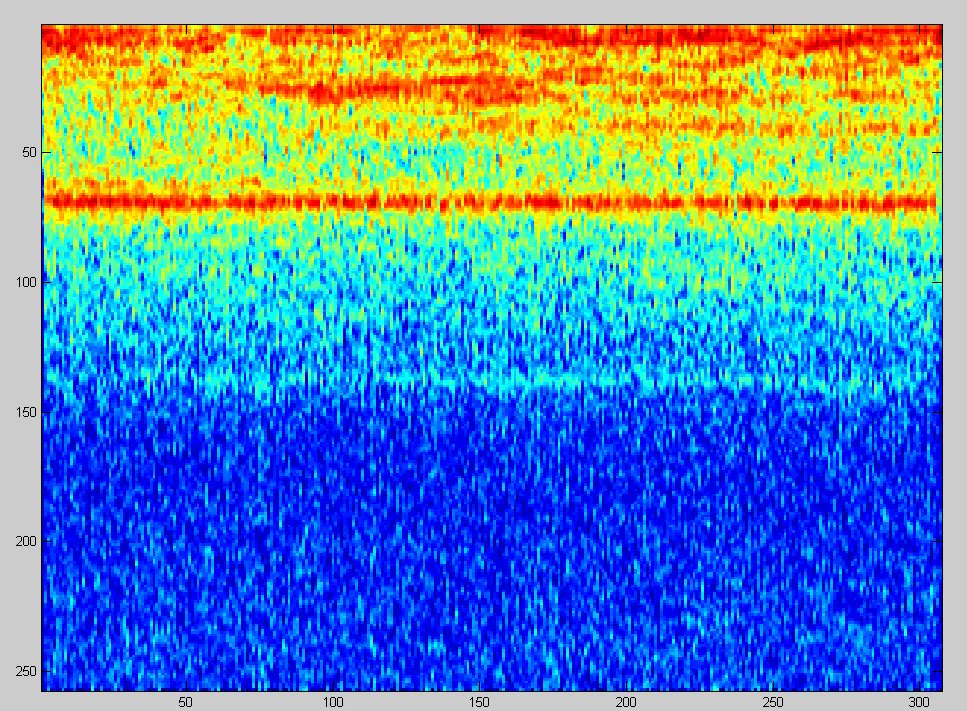
Ο οριζόντιος άξονας εδώ, όπως σε όλα τα γραφήματα, αντιπροσωπεύει τον χρόνο, ο κάθετος άξονας αντιπροσωπεύει ένα πολλαπλάσιο της περιόδου (αν και μπορούμε επίσης να μιλήσουμε για συχνότητα) του θεμελιώδους τόνου, και το χρώμα αντιπροσωπεύει την ένταση. Η σταθερή οριζόντια ευθεία γραμμή καταδεικνύει τη σταθερότητα της ταχύτητας του κινητήρα. Η πληθώρα των παραπάνω τεχνουργημάτων αξίζει να αγνοηθεί, καθώς έγραψα αυτό το πρόγραμμα για μια εντελώς διαφορετική ερευνητική εργασία.
Μια άλλη ηχογράφηση από ένα ουκρανικό drone δείχνει ξεκάθαρα το φαινόμενο Doppler κατά τη διάρκεια της πτήσης του.
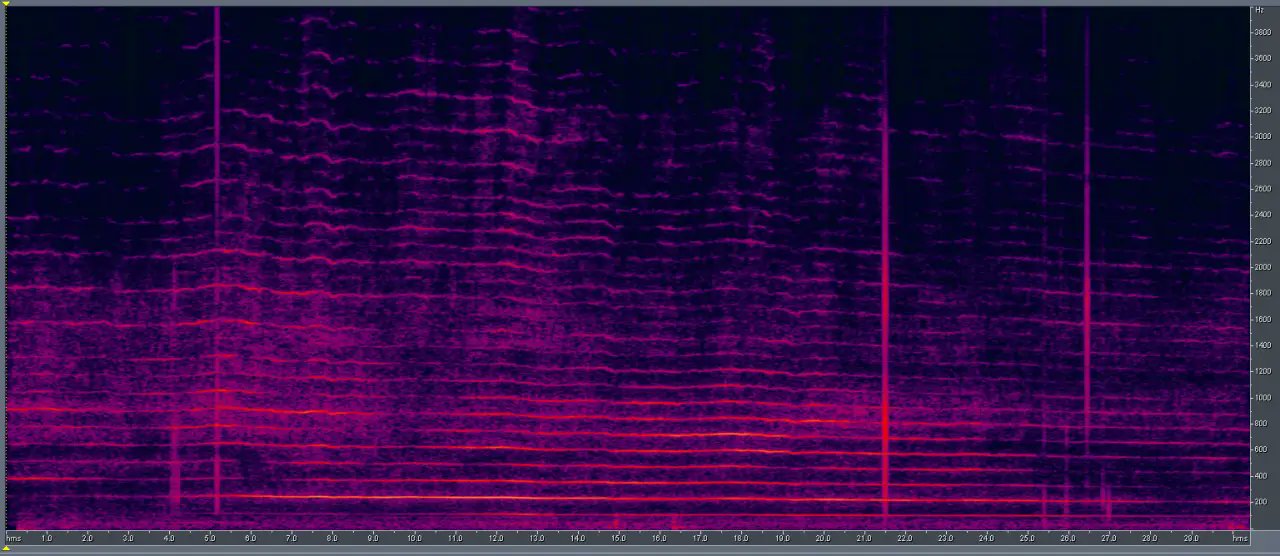
Και στο κέστρουμ βλέπουμε μια γραμμική αλλαγή στη θέση της περιόδου της θεμελιώδους συχνότητας.
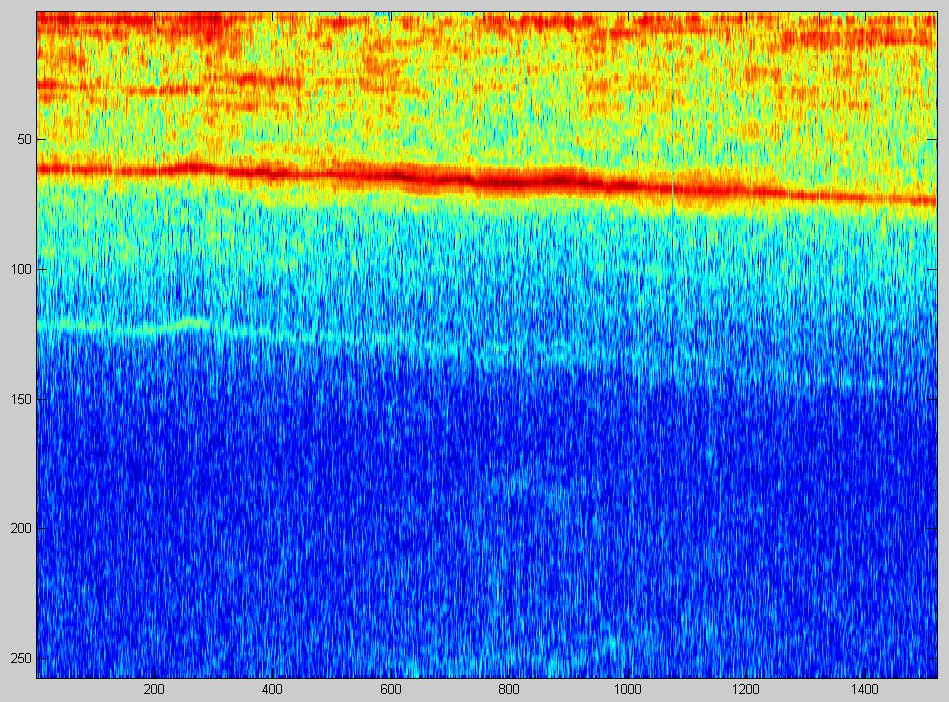
Το ενδιαφέρον μας για το κέπστρουμ πηγάζει από το γεγονός ότι μια μεγάλη ροή δεδομένων από ένα μικρόφωνο τελικά περιορίζεται στην παρατήρηση ενός μοναδικού, διακριτού σημείου. Αυτό «συσκευάζει» τα δεδομένα και επιτρέπει μια σημαντική μείωση στις ταχύτητες μετάδοσης μέσω του καναλιού επικοινωνίας. Ωστόσο, αν χρησιμοποιήσουμε το κέπστρουμ για να προσδιορίσουμε τη θεμελιώδη συχνότητα και να λάβουμε μια εικόνα Fourier όχι από ένα, αλλά από δύο μικρόφωνα με μικρή απόσταση, θα λάβουμε σχεδόν πανομοιότυπες εικόνες πλάτους, αλλά οι αρμονικές φάσεις θα διαφέρουν (η διαφορά φάσης είναι το γινόμενο του αρμονικού αριθμού, της θεμελιώδους συχνότητας και της χρονικής καθυστέρησης).
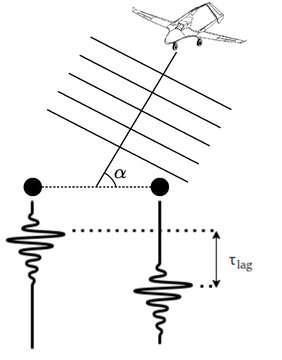
Μπορούμε να μηδενίσουμε με βίαιο τρόπο ολόκληρο το φάσμα των εξωγενών σημάτων, να ορίσουμε τα πλάτη των αρμονικών σε μια σταθερή τιμή για όλες τις αρμονικές και να χρησιμοποιήσουμε τη διαφορά φάσης μεταξύ των μικροφώνων για κάθε αρμονική συχνότητα ως φάση.
Αν "σύρουμε" αυτόν τον συνδυασμό πίσω στον μετασχηματισμό Fourier (με είσοδο μιγαδικού αριθμού), τότε για κάποια έξοδο Fourier, οι αρμονικές φάσεις θα αθροίζονται σε μια κορυφή (αν και αδύναμη), και αυτό θα μας δώσει την κατεύθυνση της πηγής ακουστικού σήματος. Αυτή η κορυφή είναι επίπεδη και όχι πολύ βολική, αλλά για κάποια άλλη έξοδο, οι αρμονικές θα αθροίζονται ως "φάση-αντιφάση", με αποτέλεσμα ένα απότομο ελάχιστο που μπορεί να χρησιμοποιηθεί για τον προσδιορισμό της κατεύθυνσης της πηγής ήχου.
Εργάζομαι για μια μεγάλη ιδιωτική εταιρεία. Εδώ, μερικές φορές εμφανίζονται πολύ δύσκολα προβλήματα στον ορίζοντα και απαιτείται υψηλός βαθμός προετοιμασίας για τις λύσεις τους. Ένα από τα ερευνητικά μου έργα πρωτοβουλίας ήταν μια εργασία με προσωρινό τίτλο "μικρόφωνο κατεύθυνσης". Όλες οι ιδέες που περιγράφονται παραπάνω έχουν τις ρίζες τους σε αυτήν την εργασία. Η ίδια η εργασία σταμάτησε επειδή εξερευνούσα διάφορες προσεγγίσεις (στην πράξη, μόνο μία ιδέα από τις τρεις έως πέντε επιβιώνει και επιτυγχάνει ένα πολύτιμο αποτέλεσμα). Οι ιδέες που αφομοίωσα από τις διαλέξεις του Κρατικού Πανεπιστημίου της Μόσχας (το κανάλι YouTube izoalex) απέδωσαν σημαντικά καλύτερα αποτελέσματα στις εργασίες μας (παρεμπιπτόντως, οι ίδιοι καθηγητές δημιούργησαν το λογισμικό iZotope RX, έναν παγκόσμιο ηγέτη στον τομέα του και... μια αμερικανική εταιρεία).
Ανάμεσα σε όλα αυτά τα προβλήματα, τα ελικόπτερα, φυσικά, ξεχωρίζουν, δημιουργώντας τις μεγαλύτερες προκλήσεις για τους φοιτητές μας. Το ηχητικό φασματογράφημα ενός ελικοπτέρου μοιάζει με αυτό:
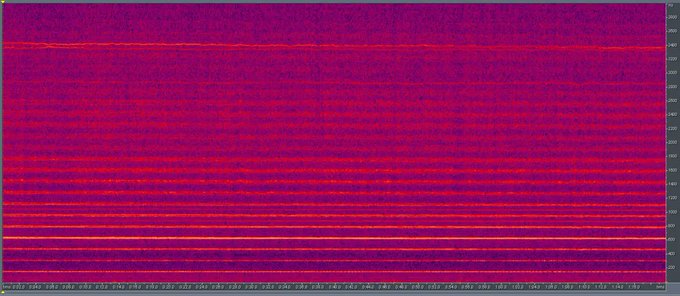
Αυξήθηκε στο τμήμα χαμηλών συχνοτήτων:
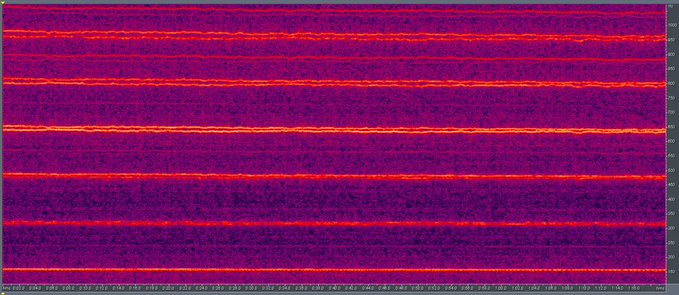
Σε αυτήν την περίπτωση, το κέπστρουμ μοιάζει με:
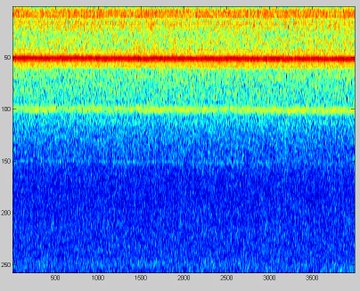
Ότι όλα αυτά θα μπορούσαν να εξαχθούν πρακτικά
1. Όλες αυτές οι λειτουργίες που αναφέρονται παραπάνω για την έκδοση 4 μικροφώνων (2 μικρόφωνα είναι ανεπαρκή λόγω μειωμένης γωνιακής ανάλυσης σε ένα συγκεκριμένο εύρος κατευθύνσεων και έλλειψης διαχωρισμού των συνδυασμών κατόπτρων) απαιτούν υπολογιστική ισχύ περίπου ισοδύναμη με τους μικροελεγκτές STM32F4xx ή STM32F7xx (αυτό βλέπουμε στους ελεγκτές πτήσης ελικοπτέρων).
Η αναμενόμενη καθυστέρηση επεξεργασίας σήματος θα είναι περίπου 30-60 χιλιοστά του δευτερολέπτου.
2. Δεν εργάζονται και σπουδάζουν πολλοί άνθρωποι στη χώρα μας στον τομέα της ψηφιακής επεξεργασίας σήματος (DSP). Οι καθηγητές πανεπιστημίου θα μπορούσαν, για παράδειγμα, να λάβουν στερεοφωνικές ηχογραφήσεις (μορφή .wav, στις οποίες η φάση δεν αφαιρείται λόγω συμπίεσης) ενός ιπτάμενου ελικοπτέρου και να δουν τι είναι ικανοί να κάνουν.
Η δυσκολία εδώ έγκειται στο γεγονός ότι η θεωρία επεξεργασίας σήματος είναι αρκετά εκτενής, πολύπλοκη και βασίζεται σε μεγάλους όγκους ποικίλων μαθηματικών. Ο δεύτερος παράγοντας που περιπλέκει την κατάσταση είναι ότι ο επαγγελματικός προγραμματισμός σε αυτόν τον τομέα απέχει εξαιρετικά πολύ από αυτό που κάνουν οι συνηθισμένοι προγραμματιστές.
Η έλλειψη τέτοιων ηχογραφήσεων (ακόμα και σε στερεοφωνική μορφή .wav από ένα ζευγάρι μικροφώνων σε απόσταση) είναι αυτό που με εμπόδισε να γράψω μια συνέχεια αυτού του άρθρου.
Η έρευνα του Γεωργίου Δικαίου: Η δυσκολία που με εμπόδισε να ανακαλύψω drones με ένα κινητό ήταν αυτό και όταν τα κατάφερα με πολλούς λανθασμένους συναγερμούς ή αστοχίες, ήταν σε πολύ χαμηλή απόσταση από εμένα και το κινητό. Η χρήση πολλαπλών μικροφώνων σε μεγάλη απόσταση 4 ή περισσότερα, θα βελτίωνε την κατάσταση αλλά όχι πολύ γιατί δεν μπορείς να τα τοποθετήσεις πολύ μακριά από το κινητό τηλέφωνο.
Η χρήση συσκευής εντοπισμού πουλιών με το κελάηδισμα που δοκίμασα, είχε μικρή αύξηση κατά 10-20 φορές των ήχων και μονοκύαλι. Κάτι τέτοιο είναι εφικτό να βελτιώσει την διαδικασία, πρέπει όμως συνεχώς να την κρατάς στο χέρι σου και να ψάχνεις. Το κόστος όμως είναι για την συσκευή από την Κίνα στα 100 ευρώ, αλλά θέλεις εκπαίδευση για να μάθεις να εντοπίζεις τους ήχους. Η συσκευή δεν ήταν δική μου και τα ακουστικά συνεχώς στα αυτιά, μια έκρηξη σε κοντινή απόσταση θα δημιουργούσε ακουστικό πρόβλημα σε όποιον φορούσε τα ακουστικά. Ίσως μια τέτοια συσκευή συνδεδεμένη με ένα κινητό να εντόπιζε τον ήχο ενός drone από μακριά.
Αναφέρομαι σε φτηνές λύσεις για έναν έφεδρο μαχητή και όχι σε πολύπλοκα συστήματα.
Αναμένουμε τα σχόλιά σας στο Twitter!